DETERMINAN MATRIKS

-
DETERMINAN MATRIKS


DEFINISI
Pada aljabar linier, determinan matriks dapat diartikan sebagai nilai yang mewakili sebuah matriks bujur sangkar. Simbol nilai determinan matriks A dinyatakan sebagai det(A) atau   \left| A \right|.  Cara menghitung determinan matriks tergantung ukuran matriks bujur sangkar tersebut, karena cara menghitung nilai determinan dengan ordo 3 akan berbeda dengan cara menghitung matriks bujur sangkar dengan ordo 2.

1. Determinan Matriks Ordo 2 x 2

{\displaystyle {\begin{aligned}|A|={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.\end{aligned}}}
matriks ordo 2 dinyatakan seperti bentuk di bawah.
  
\[ \textrm{A} \; = \; \begin{bmatrix} a & b \\ c & d \end{bmatrix} \]

Nilai determinan A disimbolkan dengan \left| A \right|, cara menghitung nilai determinan A :

  
\[ det(A) \; = \; \left| A \right| = ad - bc \]

2. Determinan Matriks Ordo 3 x 3

{\displaystyle {\begin{aligned}|A|={\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a\,{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b\,{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c\,{\begin{vmatrix}d&e\\g&h\end{vmatrix}}\\&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}}}


Matriks Ordo 3 adalah matriks bujur sangkar dengan banyaknya kolom dan baris sama dengan tiga. Bentuk umum matriks ordo 3 sebagai berikut.
  \[ \textrm{A} \; = \; \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \]
Cara menghitung determinan pada matriks dengan ordo tiga biasa disebut dengan Aturan Sarrus. 

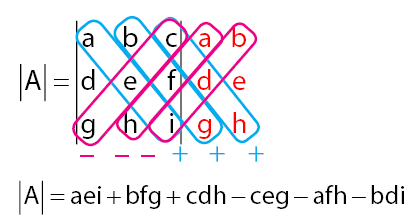
determinan matriks

METODE SARRUS
Metode sarrus adalah salah satu cara untuk mencari suatu determinan matriks yang hanya dapat digunakan untuk mencari determinan matriks ber ordo sampai dengan 3 (dimensi 3x3).
\begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{bmatrix}
maka dengan metode sarrus yaitu,
matriks_sarrus
Maka diperoleh,
det(A) = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32}- a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}- a_{12}a_{21}a_{33}
Minor entri a_{11} yaitu M_{11} = \begin{vmatrix} a_{22} & a_{23}\\ a_{32} & a_{33} \end{vmatrix} = a_{22}a_{33}-a_{23}a_{32}.
Minor entri a_{12} yaitu M_{12} = \begin{vmatrix} a_{21} & a_{23}\\ a_{31} & a_{33} \end{vmatrix} = a_{21}a_{33}-a_{23}a_{31}.
Minor entri a_{13} yaitu M_{13} = \begin{vmatrix} a_{21} & a_{22}\\ a_{31} & a_{32} \end{vmatrix} = a_{21}a_{32}-a_{22}a_{31}.
Kofaktor a_{11} yaitu C_{11} = (-1)^{1+1} M_{11} = a_{22}a_{33}-a_{23}a_{32}.
Kofaktor a_{12} yaitu C_{12} = (-1)^{1+2} M_{12} = a_{23}a_{31}-a_{21}a_{33}.
Kofaktor a_{13} yaitu C_{13} = (-1)^{1+3} M_{13} = a_{21}a_{32}-a_{22}a_{31}.
Sehingga diperoleh,
det(A) = a_{11}C_{11} + a_{12}C_{12} + a_{13}C_{13}
= a_{11}(a_{22}a_{33}-a_{23}a_{32}) + a_{12}(a_{23}a_{31}-a_{21}a_{33}) + a_{13}(a_{21}a_{32}-a_{22}a_{31})
= a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32} + a_{12}a_{23}a_{31}-a_{12}a_{21}a_{33} + a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}


METODE EKSPANSI LAPLACE
jika, A=[aij] (nxn) adalah matrik bujur sangkar berordo (nxn).
(1). Minor elemen matrik A baris ke-i dan kolom ke-j (a-ij) ditulis Mij didefinisikan sebagai determinan matrik berordo (n-1)x(n-1) yang diperoleh dari A dengan cara menghilangkan baris ke-I dan kolom ke-j.
(2). Kofaktor elemen matrik A baris ke-i kolom ke-j ditulis C-ij.

Contoh soal :
Ditanya : Hitung determinan matriks ?

Jawaban : 

menurut kolom 1

= a11.k11 - a21.k21 + a31.k31
= 0 - 2((6.3)-(2.8)) + 0
= -2(18-16) = -2(2) = - 4


METODE CHIO

Metode Chio merupakan salah satu metode yang dapat digunakan dalam
menentukan determinan matriks yang memiliki ordo n \times n dengan n \geq 3.

Kondensasi CHIO menyusutkan determinan matriks ordo n \times n 
menjadi ordo (n-1) \times (n-1) dan dikalikan dengan elemen a_{11}. 
Proses kondensasi ini berakhir pada determinan matriks ordo 2 \times 2.
Tanpa mengurangi perumuman, dalam tulisan ini menggunakan matriks persegi
dengan syarat elemen a_{11} \neq 0. 
Apabila nilai elemen a_{11} = 0 maka dilakukan proses operasi baris/kolom yaitu
menukarkan baris/kolom pada determinan matriks untuk memperoleh a_{11} \neq 0.




Contoh Soal :

Hitung determinan matriks A = \begin{bmatrix} -2&1&4\\ 3&-5&2\\ 5&2&1 \end{bmatrix}.
Dengan menggunakan metode CHIO, maka didapat
det(A) = \dfrac{1}{(-2)^{3-2}} \begin{vmatrix} \begin{vmatrix} -2&1\\ 3&-5 \end{vmatrix} & \begin{vmatrix} -2&4\\ 3&2 \end{vmatrix}\\ &\\ \begin{vmatrix} -2&1\\ 5&2 \end{vmatrix} & \begin{vmatrix} -2&4\\ 5&1 \end{vmatrix} \end{vmatrix}
= \dfrac{1}{-2} \begin{vmatrix} (-5)(-2)-(3)(1) & (-2)(2)-(3)(4)\\ (-2)(2)-(1)(5) & (-2)(1)-(4)(5) \end{vmatrix}
= \dfrac{1}{-2} \begin{vmatrix} 7&-16\\ -9&-22 \end{vmatrix}
= \dfrac{1}{-2} (7 \cdot -22-(-16) \cdot -9)
= \dfrac{1}{-2} (-154-144)
= \dfrac{1}{-2} (-298)
= -149

SIFAT-SIFAT DETERMINAN MATRIKS

Ada beberapa sifat – sifat determinan matriks, yaitu :
1. Apabila semua elemen dari salah satu baris atau kolom sama dengan nol, maka determinan matriks tersebut adalah nol. 
Contoh :
Misalkan  : 

2. Apabila semua elemen dari salah satu baris atau kolom itu sama dengan elemen-elemen baris atau kolom lain, maka determinan matriks tersebut adalah nol.
Contoh :
Misalkan: B =  (Sebab semua elemen baris ke-1 dan ke-3 adalah sama).

3. Apabila elemen-elemen salah satu dari baris atau kolom adalah merupakan kelipatan dari elemen-elemen baris atau kolom lain maka determinan matriks tersebut adalah nol.
Contoh : 
Misalkan: A =  (semua elemen pada baris ke-3 sama dengan kelipatan semua elemen baris ke-1).
4. |AB| : |A| ×|B|
5. |AT| = |A|, untuk AT ialah transpose dari matriks A.
6. |A–1| =  , untuk A–1 ialah invers dari matriks A.
7. |kA| = kn |A|, untuk A ordo n × n dan k adalahsuatu konstanta.






Komentar

Posting Komentar

Postingan populer dari blog ini

METODE CHIO - DETERMINAN MATRIKS

-
Gambar
METODE CHIO DALAM DETERMINAN MATRIKS Metode Chio merupakan salah satu metode yang dapat digunakan dalam menentukan determinan matriks yang memiliki ordo   dengan  . Metode Chio menyusutkan determinan matriks ordo    menjadi ordo   dan dikalikan dengan elemen  .  Proses ini berakhir pada determinan matriks ordo  . Tanpa mengurangi perumuman, dalam tulisan ini menggunakan matriks persegi dengan syarat elemen  .  Apabila nilai elemen    maka dilakukan proses operasi baris/kolom yaitu menukarkan baris/kolom pada determinan matriks untuk memperoleh  . Metode Chio ordo 3 x 3 : Metode Chio ordo 4 x 4 : U kuran matriksnya diperluas atau diperumuskan menjadi  , maka diperoleh : Rumus ini diatas, dikenal sebagai rumus menghitung determinan  dengan mereduksi orde atau matriks. Reduksi pada orde menggunakan elemen matriks yang lain dan tidak har...
Baca selengkapnya

INVERS MATRIKS

-
Gambar
INVERS  MATRIKS A. DEFINISI MATRIKS     Invers matriks bisa didefinisikan dimana jika A merupakan suatu matriks kuadrat, maka anda bisa mencari matriks B dengan AB = BA = I . A dikatakan bisa dibalik dan B disebut dengan invers dari A.   Matriks yang mempunyai invers disebut sebagai invertible atau matriks non singular, sedangkan matriks yang tidak mempunyai invers disebut matriks singular. 1. Ma trik bujur sangkar A dikatakan mempunyai invers , jika terdapat matrik B   sedemikian          rupa sehingga :      AB = BA = I     dimana I matrik identitas 2. B dikatakan invers matrik A ditulis A –1 , maka , AA –1 = A –1 A = I 3. A dikatakan invers matrik B d itulis B –1 , maka , B –1 B= BB –1 = I Untuk mencari invers matriks persegi berordo 2x2: Jika   dengan  , maka invers matriks A (ditulis  ) adalah sebagai berikut: Jika   mak...
Baca selengkapnya

MATRIKS DAN JENIS-JENIS MATRIKS

-
Gambar
MATRIKS DAN JENIS-JENIS MATRIKS DEFINISI MATRIKS Dalam matematika, "Matriks adalah kumpulan bilangan, simbol, atau ekspresi, berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks." Pada umumnya matriks dapat diartikan sebagai suatu susunan atau kumpulan dari beberapa bilangan yang disusun berdasarkan kepada baris dan kolom yang berbentuk persegi panjang. Matriks memiliki ciri khas khusus dimana biasanya bilangan yang menjadi elemen dari sebuah matriks disusun dengan diapit oleh tanda kurung siku [] namun terkadang ada juga elemen matriks yang diapit oleh tanda kurung biasa (). Ukuran dari sebuah matriks disebut sebagai ordo yang menjelaskan jumlah dari kolom dan baris yang ada di dalam matriks tersebut.  Ukuran dari sebuah matriks dapat di simbolkan dengan rumus : A mxn Diketahui :  A = Nama Matriks m = jumlah baris n = jumlah ko...
Baca selengkapnya