SIFAT-SIFAT DAN DEKOMPOSISI DETERMINAN MATRIKS
- Dapatkan link
- X
- Aplikasi Lainnya
SIFAT-SIFAT DAN DEKOMPOSISI PADA
DETERMINAN MATRIKS
SIFAT-SIFAT DETERMINAN MATRIKS
Pada determinan matriks memiliki sifat-sifat. Sifat-sifat pada determinan matriks sangat bermanfaat ketika menghitung matriks-matriks dengan karakteristik yang khusus, seperti matriks dengan elemen nol, matriks segitiga atas/bawah, dan matriks dengan baris sebanding.
Ada beberapa sifat – sifat determinan matriks, yaitu :
1. Apabila semua elemen dari salah satu baris atau kolom sama dengan nol, maka determinan matriks tersebut adalah nol.
Contoh :
Misalkan : 
2. Apabila semua elemen dari salah satu baris atau kolom itu sama dengan elemen-elemen baris atau kolom lain, maka determinan matriks tersebut adalah nol.
Contoh :
Misalkan: B =  (Sebab semua elemen baris ke-1 dan ke-3 adalah sama).
(Sebab semua elemen baris ke-1 dan ke-3 adalah sama).
3. Apabila elemen-elemen salah satu dari baris atau kolom adalah merupakan kelipatan dari elemen-elemen baris atau kolom lain maka determinan matriks tersebut adalah nol.
Contoh :
Misalkan: A =  (semua elemen pada baris ke-3 sama dengan kelipatan semua elemen baris ke-1).
(semua elemen pada baris ke-3 sama dengan kelipatan semua elemen baris ke-1).
4. |AB| = |A| ×|B|
Contoh :

Contoh :
5. |AT| = |A|, untuk AT adalah transpose dari matriks A.
![\[ \left( A + B \right) ^{T} = A^{T} + B^{T} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-4ee5d4ebea15ca7b66d0c3123697241a_l3.svg)
![\[ (AB )^{T} = B^{T} A^{T} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-5052f0ca27b9622c4774984915b5ce90_l3.svg)
Contoh :
Diketahui dengan Matriks 3 x 2 ,
![\[ \textrm{A} \; = \; \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-a8041d0b9ed91363ca9f0ab01da0f42a_l3.svg)
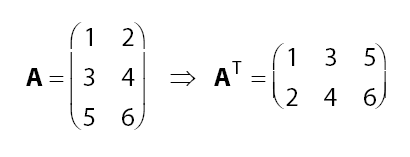
Contoh :
Diketahui dengan Matriks 3 x 2 ,
Maka matriks transpose A adalah:
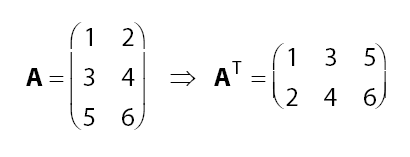
6. |A–1| =  , untuk A–1 adalah invers dari matriks A.
, untuk A–1 adalah invers dari matriks A.
Contoh :
Matriks 3 x 3



Contoh :
Matriks 3 x 3
Matriks B
Tukar Baris
Tukar Kolom
7. |kA| = kn |A|, untuk A ordo n × n dan k adalah suatu konstanta.
Contoh :
Matriks 3 x 3
Matriks B
B' (baris)
B' (Kolom)
DEKOMPOSISI MATRIKS DAN DETERMINAN
Matriks bujur sangkar A dikatakan didekomposisi, jika matriks segitiga bawah L dan
matriks segitiga bawah U .
A = LU
Maka,
det(A) = det(L) det(U)
Beberapa teknik menghitung dekomposisi determinan matriks :
1. Metode Crout
Matriks Ordo 3 x 3

Rumus perhitungan :

2. Metode Doolittle
Metode Ordo 3 x 3

Rumus Perhitungannya,

3. Metode Cholesky
Metode cholesky adalah sebuah penyelesaian persamaan linier simultan yang diperoleh dari rumusan matematika berdasarkan atas unsur koefisien variabel yang simetris.Matriks yang diselesaikan harus matriks yang berordo sama atau yang biasa disebut adalah matriks simetris. Unsur matriks baris sama dengan unsur matriks kolom pada indeks baris dan kolom yang sama. Nilai di dalam tanda akar harus bernilai positif. Angka diluar diagonal utama harus memiliki nilai yang sama.
[A] = [U] * [UT]
Dimana:
[A] = Nilai Matrik Soal
[U] = Nilai Matrik Segitiga Atas
[UT] = Nilai Matrik Segitiga Bawah
4. Metode Operasi Elementer
Contoh :
Carilah solusi dari persamaan dibawah ini ,
Penyelesaian :
Mengubah persamaan tersebut kedalam bentuk matriks yang diperbesar ,
kemudian :
- baris kedua : B2 + (-2)B1,baris ketiga : B3 + (-3)B1,
- baris kedua : B2 x (1/2),
- baris ketiga : B3 + (-3)B2,
- baris ketiga : B3 x 2,
pada matriks terakhir ini dinamakan matriks berada dalam bentuk eselon baris. Dari matriks eselon baris ini dapat ditulis kedalam bentuk persamaan yang bersesuaian dengan matriks tersebut.
sehingga dengan mensubstitusikan  kedalam persamaan kedua, diperoleh
kedalam persamaan kedua, diperoleh  . Setelah itu substitusikan
. Setelah itu substitusikan  dan
dan  kepersamaan pertama, diperoleh $latex x + 2 + 2(3) = 9 .
kepersamaan pertama, diperoleh $latex x + 2 + 2(3) = 9 .
Jadi, solusi dari persamaan diatas adalah  ,
,  dan
dan  .
.
- Dapatkan link
- X
- Aplikasi Lainnya

Komentar
Posting Komentar