INVERS MATRIKS
INVERS MATRIKS
A. DEFINISI MATRIKS
Invers matriks bisa didefinisikan dimana jika A merupakan suatu matriks kuadrat, maka anda bisa mencari matriks B dengan AB = BA = I. A dikatakan bisa dibalik dan B disebut dengan invers dari A. Matriks yang mempunyai invers disebut sebagai invertible atau matriks non singular, sedangkan matriks yang tidak mempunyai invers disebut matriks singular.
1. Matrik bujur sangkar A dikatakan mempunyai invers, jika terdapat matrik B sedemikian rupa sehingga :
AB = BA
= I
dimana I matrik identitas
2. B dikatakan invers matrik A ditulis A–1, maka, AA–1 = A–1A = I
3. A dikatakan invers matrik B ditulis B–1, maka, B–1B= BB–1 = I
Untuk mencari invers matriks persegi berordo 2x2:
Jika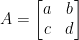
dengan 
, maka invers matriks A (ditulis 
) adalah sebagai berikut:
Jika
dengan , maka invers matriks A (ditulis 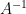) adalah sebagai berikut:
Jika 
maka matriks tidak dapat mempunyai invers, atau biasa disebut
dengan matriks singular.
maka matriks tidak dapat mempunyai invers, atau biasa disebutdengan matriks singular.
Sifat-sifat matriks persegi mempunyai invers sebagai berikut:
%5E%7B-1%7D+%3D+B%5E%7B-1%7D+%5Ccdot+A%5E%7B-1%7D&bg=T&fg=000000&s=0 "(A \cdot B)^{-1} = B^{-1} \cdot A^{-1}")
%5E%7B-1%7D+%3D+A%5E%7B-1%7D+%5Ccdot+B%5E%7B-1%7D&bg=T&fg=000000&s=0 "(B \cdot A)^{-1} = A^{-1} \cdot B^{-1}")
%5Et+%3D(A%5E%7Bt%7D)%5E%7B-1%7D&bg=T&fg=000000&s=0 "(A^{-1})^t =(A^{t})^{-1}")
Pada invers matriks dapat dihitung melalui dengan metode :
Metode Adjoint Matriks
Jika A matrik bujur sangkar berordo (nxn), Cij=(-1)i+j Mij kofaktor elemen matrik aij.
transpose dari matriks yang elemen-elemennya merupakan kofaktor-kofaktor dari elemen-elemen matriks A, yaitu :
adj(A) = (kof(A))T
Untuk rumus invers matriks :
Keterangan :
A-1 : Invers Matriks (A)
Det (A) : Determinan Matriks (A)
Adj (A) : Adjoin Matriks (A)
Dari rumus tersebut, cara mencari dalam metode adjoint adalah sebagai :
Agar lebih memahami mengenai metode adjoint dapat diperhatikan dalam contoh berikut ini :
--TERIMA KASIH--
Komentar
Posting Komentar